ISC Class 12th Computer Science Paper 1 Exam 2024 : Most Important Question with Solution for Last-Minute Revision

SHARING IS CARING
If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.
ISC Class 12 exams have started and you have very little time left for the Computer Science – Paper 1 exam. Therefore, we are providing important Multiple Choice Questions, Fill in the Blanks, Short Answer Type Questions, Long Answer Type Questions in this article. You can study them well and score well in your exams.
To help you prepare effectively, we have prepared a list of important multiple-choice questions (MCQs) with detailed explanations. This guide aims to make your exam preparation easier by providing information on these questions.
These questions cover various topics from the Computer Science – Paper 1 syllabus. Remember, it is important to understand the logic behind each answer to score well.
ISC Class 12th Computer Science – Paper 1 Most Important Question
Question - 1
(i) Absorption law states that :
(a) A • ( Aꞌ + B) = A
(b) A + ( A • B) = A
(c) Both (a) and (b)
(d) A • ( B + C ) = A • B + A • C
(ii) Assertion : A=0 B=1 C=0 and D=1 and minterm is Aꞌ•B•Cꞌ•D
Reason : The final sum term must be 0 so A and C are complemented.
Which one of the following options is correct ?
(a) Both Assertion and Reason are true, and Reason is the correct explanation for Assertion.
(b) Both Assertion and Reason are true, but Reason is not the correct explanation for Assertion.
(c) Assertion is true and Reason is false.
(d) Assertion is false and Reason is true.
(iii) According to the Principle of duality, the Boolean equation
(P + Qꞌ) • R • 1 = P • R + Qꞌ • R will be equivalent to :
(a) P • Qꞌ + R + 1 = (P + R) • (Qꞌ + R)
(b) P • Qꞌ + R + 0 = (P + R) • (Qꞌ + R)
(c) Pꞌ • Q + R + 1 = (Pꞌ • Rꞌ) • (Q + Rꞌ)
(d) P • Qꞌ + R • 0 = (P + R) • (Qꞌ + R)
(iv) The complement of the Boolean expression (X • Y)′ + Z′ is :
(a) (X + Y) • Z
(b) X • Y • Z
(c) (Xꞌ + Yꞌ) • Zꞌ
(d) (Xꞌ + Yꞌ) • Z
(v) The equivalent of P ˄ Q ˅ ~ P ˄ ~ Q will be :
(a) ( ( P ˄ Q ) ˅ ~ P ) ˄ ~ Q
(b) ( P ˄ Q ) ˅ ( ~ P ˄ ~ Q )
(c) P ˄ ( Q ˅ ~ P ) ˄ ~ Q
(d) P ˄ ( Q ˅ (~ P ˄ ~ Q ) )
(vi) Assertion : Boolean algebra and Binary number system are different from each other.
Reason : There are some basic operations like AND, OR and NOT which are performed only in Boolean algebra.
(a) Both Assertion and Reason are true, and Reason is the correct explanation for Assertion.
(b) Both Assertion and Reason are true, but Reason is not the correct explanation for Assertion.
(c) Assertion is true and Reason is false.
(d) Assertion is false and Reason is true.
(vii) What is the relevance of the keyword static for a data member of a class.
(viii) State any one purpose of using interfaces in Java programming.
(ix) Define Canonical form of an expression with respect to its Cardinal form.
(x) State any one application each of half adder and full adder.
Question - 2
(i) Convert the following infix notation to postfix form.
( A / B + C ) / ( D * ( E − F )
(ii) An array ARR[ −4 …..6, −2…..12] , stores elements in Row Major Wise, with the address ARR[2][3] as 4142. If each element requires 2 bytes of storage, find the Base address.
(iii) The following functions are a part of some class :
void Try(char ch[],int x)
{ System.out.println(ch); char temp;
if ( x<ch.length/2)
{ temp=ch[x];
ch[x]= ch[ch.length-x-1];
ch[ch.length-x-1] = temp;
Try(ch,x+1);
} }
void Try1(String n)
{ char c[]=new char[n.length()];
for(int i=0;i<c.length;i++)
c[i] = n.charAt(i);
Try(c,0);
}
(a) What will the output of Try( ) when the value of ch[]={‘P’, ‘L’,‘A’, ‘Y’} and x=1 ?
(b) What will the output of Try1( ) when the value of n=”SKY” ?
(iv) The following function is a part of some class which computes and returns the value of a number ‘p’ raised to the power ‘q’ (p q ). There are some places in the code marked by ?1? , ?2? , ?3? which must be replaced by an expression / a statement so that the function works correctly.
double power ( double p , int q )
{ double r = ?1? ;
int c = ( q<0 ) ? -q : q ;
if ( q == 0)
return 1 ;
else
{ for (int i = 1; i <= c ;?2?, i++);
return (q>0)? r : ?3?;
}
}
(a) What is the expression or statement at ? 1 ?
(b) What is the expression or statement at ? 2 ?
(c) What is the expression or statement at ? 3 ?
Question - 3
(i) A Football Association coach analyses the criteria for a win/draw of his team depending on the following conditions.
• If the Centre and Forward players perform well but Defenders do not perform well.
OR
• If Goalkeeper and Defenders perform well but the Centre players do not perform well.
OR
• If all perform well.
The inputs are :
| INPUTS | |
| C | Centre players perform well |
| D | Defenders perform well |
| F | Forward players perform well |
| G | Goalkeeper perform well |
(In all the above cases, 1 indicates yes and 0 indicates no.)
Output : X - Denotes the win/draw criteria [1 indicates win/draw and 0 indicates defeat in all cases]
Draw the truth table for the inputs and outputs given above and write the SOP expression for X(C, D, F, G).
(ii) Reduce the above expression X (C, D, F, G) by using 4-variable Karnaugh map, showing the various groups (i.e. octal, quads and pairs).
Draw the logic gate diagram for the reduced expression. Assume that the variables and their complements are available as inputs.
Question - 4
(i) (a) Reduce the Boolean function F(A,B,C,D) = π (0, 1, 2, 3, 4, 6, 9, 11, 13) by using 4-variable Karnaugh map, showing the various groups (i.e. octal, quads and pairs).
(b) Draw the logic gate diagram for the reduced expression. Assume that the variables and their complements are available as inputs.
(ii) (a) From the logic circuit diagram given below, name the outputs (1), (2) and (3) and finally derive the Boolean expression (F) and simplify it. Identify the propositional connective which is equivalent to the simplified Boolean expression.
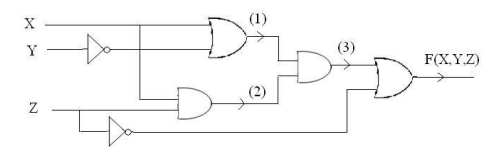
(b) If A=1 and B=0 then find the value of (Aꞌ + 1) • B
Question - 5
(i) Draw the logic circuit to encode the following Hexadecimal number (1, 3, 5, 6, 9, A, C, E) to its binary equivalents. Also state the binary equivalents of the given numbers.
(ii) Verify if the following proposition is valid using the truth table : A => ( B ∧ C ) = ( A => B ) ∧ ( B => C )
(iii) How is a 2 to 4 decoder related to 4:1 multiplexer ?
Question - 6
An Evil Number is a number which contains even number of 1’s in its binary equivalent.
Example : Binary equivalent of 10 = 1010 which contains even number on 1’s. Thus, 10 is an Evil Number.
Design a class Evil to check if a given number is an Evil number or not. Some of the members of the class are given below : .
Class name : Evil
Data members/instance variables :
num : to store a positive integer number
bin : to store the binary equivalent
Methods / Member functions :
Evil( ) : default constructor to initialize the data member with legal initial value
void acceptNum( ) : to accept a positive integer number
void rec_bin (int x) : to convert the decimal number into its binary equivalent using recursive technique
void check( ) : to check whether the given number is an Evil number by invoking the function rec_bin() and to display the result with an appropriate message
Specify the class Evil giving details of the constructor( ), void acceptNum( ), void rec_bin(int) and void check( ). Define a main( ) function to create an object and call all the functions accordingly to enable the task.
Question - 7
A class Composite contains a two-dimensional array of order [m x n]. The maximum values possible for both ‘m’ and ‘n’ is 20. Design a class Composite to fill the array with the first (m x n) composite numbers in column wise.
[Composite numbers are those which have more than two factors.]
The details of the members of the class are given below :
Class name : Composite
Data members/instance variables :
arr[ ] [ ] : integer array to store the composite numbers column wise
m : integer to store the number of rows
n : integer to store the number of columns
Member functions/methods :
Composite(int mm, int nn ) : to initialize the size of the matrix, m=mm and n=nn
int isComposite( int p ) : to return 1 if the number is composite otherwise returns 0
void fill ( ) : to fill the elements of the array with the first (m × n) composite numbers in column wise
void display( ) : to display the array in a matrix form
Specify the class Composite giving details of the constructor(int,int), int isComposite(int), void fill( ) and void display( ). Define a main( ) function to create an object and call all the functions accordingly to enable the task.
Question - 8
A class Encode has been defined to replace only the vowels in a word by the next corresponding vowel and form a new word.
i.e. A → E, E → I, I → O, O → U, U → A and a → e, e → i, i → o, o → u, and u → a
Example : Input : Institution
Output : Onstotatoun
Some of the members of the class are given below :
Class name : Encode
Data members/instance variables:
word : to store a word
length : integer to store the length of the word
new_word : to store the encoded word
Methods / Member functions :
Encode( ) : default constructor to initialize data members with legal initial values
void acceptWord( ) : to accept a word
void nextVowel( ) : to replace only the vowels from the word stored in ‘word’ by the next corresponding vowel and to assign it to ‘newword’, with the remaining alphabets unchanged
void display( ) : to display the original word along with the encrypted word
Specify the class Encode giving details of the constructor( ), void acceptWord( ), void nextVowel( ) and void display( ). Define a main ( ) function to create an object and call the functions accordingly to enable the task.
Question - 9
Shelf is a kind of data structure which can store elements with the restriction that an element can be added from the rear end and removed from the front end only.
The details of the class Shelf are given below :
Class name : Shelf
Data members/instance variables :
ele[ ] : array to hold decimal numbers
lim : maximum limit of the shelf
front : to point the index of the front end
rear : to point the index of the rear end
Methods / Member functions :
Shelf(int n ) : constructor to initialize lim=n, front= 0 and rear=0
void pushVal(double v) : to push decimal numbers in the shelf at the rear end if possible, otherwise display the message “ SHELF IS FULL ”
double popVal( ) : to remove and return the decimal number from the front end of the shelf if any, else returns −999.99
void display( ) : to display the elements of the shelf
(i) Specify the class Shelf giving details of the functions void pushVal(double) and double popVal( ). Assume that the other functions have been defined.
The main( ) function and algorithm need NOT be written.
(ii) Name the entity described above and state its principle.
Question - 10
A super class Circle has been defined to calculate the area of a circle. Define a subclass Volume to calculate the volume of a cylinder.
The details of the members of both the classes are given below :
Class name : Circle
Data members/instance variables :
radius : to store the radius in decimals
area : to store the area of a circle
Methods / Member functions :
Circle( ... ) : parameterized constructor to assign values to the data members
void cal_area() : calculates the area of a circle (πr2)
void display( ) : to display the area of the circle
Class name Volume
Data members/instance variables :
height : to store the height of the cylinder in decimals
volume : to store the volume of the cylinder in decimals
Methods / Member functions:
Volume( ... ) : parameterized constructor to assign values to the data members of both the classes
double calculate( ) : to calculate and return the volume of the cylinder using the formula (πr2h) where, r is the radius and h is the height
void display( ) : to display the area of a circle and volume of a cylinder
Assume that the super class Circle has been defined. Using the concept of inheritance, specify the class Volume giving the details of the constructor(...), double calculate( ) and void display( ).
The super class, main function and algorithm need NOT be written.
Question - 11
(i) With the help of an example, briefly explain the constant factor in time complexity.
(ii) Answer the following questions from the diagram of a Binary Tree given below :
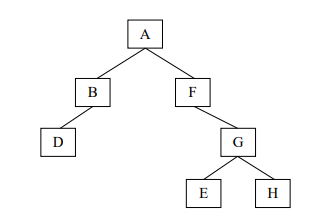
(a) Name the external nodes of the right sub tree.
(b) State the size and depth of the tree.
(c) Write the post-order traversal of the above tree structure.







 Profile
Profile Signout
Signout












 Quiz
Quiz
 Get latest Exam Updates
Get latest Exam Updates 










