UP Board 10th Maths Exam 2024 : VVI Most Important Question with Answers

SHARING IS CARING
If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.
UP बोर्ड 10वीं की गणित परीक्षा 27 फरवरी, 2024 को निर्धारित है। तो यह आर्टिकल आपके लिए काफी ज्यादा महत्वपूर्ण साबित होने वाला है क्योंकि इस आर्टिकल में आपको बोर्ड परीक्षा के लिए वो ही प्रश्न दिए गए है जो बोर्ड पेपर में आने जा रहे है।
यहाँ पर UP Board क्लास 10th के गणित (UP Board Maths Class 10th Exam 2024 VVI Most Important Question) से संबंधित महत्वपूर्ण प्रश्न दिए गए है। महत्वपूर्ण प्रश्नों का एक संग्रह है जो बहुत ही अनुभवी शिक्षकों के द्वारा तैयार किये गए है। इसमें प्रत्येक महत्वपूर्ण प्रश्नों को छांट कर एकत्रित किया गया है, जिससे कि विद्यार्थी कम समय में अच्छे अंक प्राप्त कर सके।
Read Also -
UP Board Maths Class 10th Exam 2024 VVI Most Important Question
खण्ड 'अ'
बहुविकल्पीय प्रश्न-
1. किन्हीं दो संख्याओं का LCM 60 तथा HCF 3 है । एक संख्या 12 है तो दूसरी संख्या होगी-
(i) 20
(ii) 15
(iii) 180
(iv) 36
Ans: (ii) 15
2. एक शून्येतर परिमेय संख्या और एक अपरिमेय संख्या का गुणनफल होता है-
(i) सदैव अपरिमेय संख्या
(ii) सदैव परिमेय संख्या
(iii) परिमेय या अपरिमेय संख्या
(iv) एक
Ans: (i) सदैव अपरिमेय संख्या
3. रेखायुग्म समीकरण x + 2y – 5 – 0 और 4x + 8y - 20 = 0 के हल होंगे-
(i) केवल एक अद्वितीय हल
(ii) अपरिमित रूप से अनेक हल
(iii) कोई हल नही
(iv) दो हल होंगे।
Ans: (ii) अपरिमित रूप से अनेक हल
4. वह सबसे बड़ी संख्या, जिससे 70 और 125 को विभाजित करने पर क्रमशः शेषफल 5 और 8 प्राप्त होता है-
(i) 13
(ii) 65
(iii) 875
(iv) 1750
Ans: (i) 13
5. 3 के प्रथम पाँच गुणजों का योग है-
(i) 45
(ii) 55
(iii) 65
(iv) 75
Ans: (i) 45
6. द्विघात समीकरण 2x2 – 4x + 3 = 0 के बारे में निम्न कथनों पर विचार कीजिए -
(a) दिये गये समीकरण के विविक्तकर शून्य से कम है।
(b) समीकरण के कोई मूल वास्तविक नहीं हैं ।
(c) समीकरण के विविक्तकर शून्य है ।
(d) समीकरण के मूल वास्तविक हैं ।
निम्नलिखित में से सही उत्तर का चयन कीजिए-
(i) a और b सही हैं
(11) a और d सही हैं
(iii) c और d सही हैं
(iv) केवल a सही हैं
7. AOBC एक आयत है, जिसके तीन शीर्ष A(0,3), 0(0,3) और B (5,0) हैं। इसका विकर्ण है-
(i) 5
(ii) 3
(iii) √34
(iv) 4
Ans: (iii) √34
8. यदि समीकरण x2 + kx - 5/4 = 0 का एक मूल है, तो k का मान है-
(i) 2
(ii) -2
(iii) 1/4
(iv) 1|2
Ans: (i) 2
9. दो त्रिभुज समरूप होते हैं-
(i) यदि इनके संगत कोण बराबर हों ।
(ii) इनकी संगत भुजाएँ एक ही अनुपात (समानुपाती) में होती हैं।
(iii) उपर्युक्त दोनों
(iv) इनमें से कोई नहीं ।
Ans: (i) यदि इनके संगत कोण बराबर हों ।, (ii) इनकी संगत भुजाएँ एक ही अनुपात (समानुपाती) में होती हैं।
10. यदि एक समकोण ΔABC में, ∠C = 90° AC = 3 सेमी० और BC = 4 सेमी0 है, तो बिन्दु C से जाने वाली माध्यिका की माप है-
(i) 2.5 सेमी.
(ii) 3 सेमी.
(iii) 3.5 सेमी.
(iv) 4 सेमी.
Ans: (i) 2.5 सेमी.
11. यदि (sinθ – cosθ ) = 1 है तो (sin4θ + cos4θ) का मान होगा-
(i) 1
(ii) 3/4
(iii) 1/2
(iv) 1/4
Ans: (iii) 1/2
12. sin 2A = 2sinA तब सत्य होता है, जबकि A बराबर है-
(i) 0°
(ii) 30°
(iii) 45°
(iv) 60°
Ans: (i) 0°
13. यदि 4 tanθ = 3 है, तो (4 sinθ - cosθ/ 4sin θ + cosθ) बराबर है-
(i) 2/3
(ii) 1/3
(iii) 1/2
(iv) 3/4
Ans: (iii) 1/2
14. (secA + tanA) (1-sin A) का मान होगा-
(i) sec A
(ii) sin A
(iii) cosec A
(iv) cos A
Ans: (iv) cos A
15. यदि त्रिज्या 7 से०मी० वाले एक वृत्त के एक त्रिज्यखंड का कोण 60° है। त्रिज्यखण्ड का क्षेत्रफल है-
(i) πr2θ/360°
(ii) πr2θ/180°
(iii) 2πrθ/360°
(iv) 2πrθ/180°
16. एक सुराही निम्नलिखित का संयोजन है-
(i) एक गोला और एक बेलन
(ii) एक अर्धगोला और एक बेलन
(iii) दो अर्धगोले
(iv) एक बेलन और एक शंकु
Ans: (i) एक गोला और एक बेलन
17. 1 से 10 तक की धनात्मक विषम संख्याओं का माध्य होगा-
(i) 2
(ii) 3
(iii) 4
(iv) 5
Ans: (iv) 5
18. आंकड़ो 13, 15, 16, 17, 19, 20, की माध्यिका होगी-
(i) 30/2
(ii) 31/2
(iii) 33/2
(iv) 35/2
Ans: (iii) 33/2
19. यदि कुछ प्रेक्षणों का माध्य 27 तथा बहुलक 45 है, तब माध्यिका होगी-
(i) 32
(ii) 33
(iii) 34
(iv) इनमें से काई नहीं
Ans: (ii) 33
20. जब एक पासे को फेंका जाता है, तो 3 से छोटी एक विषम संख्या आने की प्रायिकता है-
(i) 1/6
(ii) 1/3
(iii) 1/2
(iv) 0
Ans: (i) 1/6
खण्ड 'ब'
1. सभी खण्ड कीजिए-
(क) स्पष्ट कीजिए कि 3 × 5 × 7 × 7 एक भाज्य संख्या क्यों है?
Ans: हमारे पास, 3 × 5 × 7 + 7 = 7[3 × 5 + 1],
जो एक अभाज्य संख्या नहीं है क्योंकि इसका गुणनखंड 7 है,
यानी इसके दो से अधिक कारक हैं।
अतः यह एक भाज्य संख्या है।
(ख) यदि Cotθ = 7/8 तो (1+ Sinθ)(1 – Sinθ)/(1 + Cosθ) (1 - Cosθ) का मान निकालिए?
Ans: आइए एक समकोण त्रिभुज ABC पर विचार करें, जो बिंदु B पर समकोण है।

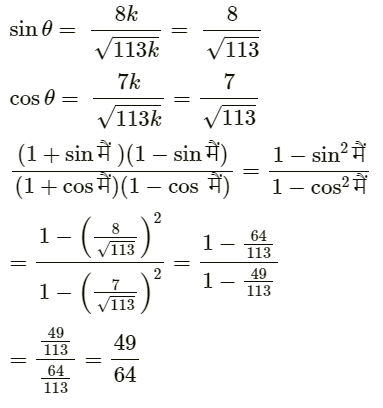
(ग) दो घनों, जिनमें से प्रत्येक का आयतन 64 से०मी० है, के संलग्न फलकों को मिलाकर एक ठोस बनाया जाता है। इससे प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए ।
Ans: मान लीजिये,
घनों का आयतन = 64 cm3
(किनारे)3 = 64
किनारा = 4 सेमी
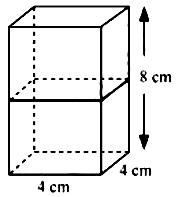
यदि घनों को एक सिरे से दूसरे सिरे तक जोड़ा जाए, तो परिणामी घनाभ की विमाएँ 4 सेमी, 4 सेमी, 8 सेमी होंगी।
∴ घनाभों का पृष्ठीय क्षेत्रफल = 2(lb+bh+lh)
= 2(4 x 4 + 4 x 8 + 4 x 8)
=2(16+32+32)
2(16+64)
= 2 x 80 = 160 सेमी2
(घ) निम्न आँकड़ों का माध्य ज्ञात कीजिए—
| वर्ग अन्तराल | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 |
| बारम्बारता | 2 | 7 | 12 | 15 | 8 | 6 |
(ड़) बिन्दु (–4, 6), बिन्दुओं A (- 6, 10) और B (3, 8) को जोड़ने वाले रेखाखण्ड को किस अनुपात में विभाजित करता है?
Ans:

(च) X और y में एक ऐसा सम्बन्ध ज्ञात कीजिए कि बिन्दु (X, y) बिन्दुओं (3,6) और (−3,4) से समदूरस्थ हो ।
Ans:

2. निम्नलिखित में से किन्हीं पाँच खण्डों को हल कीजिए-
(क) द्विघात बहुपद 6x2 – 3 - 7x के शून्यक ज्ञात कीजिए और शून्यकों तथा गुणांकों के बीच के सम्बन्ध की सत्यता की जाँच कीजिए ।
Ans:

(ख) दो संख्याओं के वर्गों का अन्तर 180 है। छोटी संख्या का वर्ग बड़ी संख्या का आठ गुना है। दोनों संख्याएँ ज्ञात कीजिए ।
Ans: माना कि बड़ी संख्या = x
तब छोटी संख्या का वर्ग = 8 गुना बड़ी संख्या = 8x
और बड़ी संख्या का वर्ग r = x
प्रश्न के अनुसार,
x - 8x = 180
=> x - 8x - 180 = 0
=> x - 18x + 10x - 180 = 0
=> x(x - 18) + 10(x - 18) = 0
=> (x - 18) (x + 10) = 0
=> x - 18 = 0 या x + 10 = 0
=> x = 18 या x = -10
इस प्रकार, बड़ी संख्या = 18 या -10
फिर, छोटी संख्या का वर्ग = 8(18) या 8(-10)
= 144 या -80 किसी संख्या का वर्ग ऋणात्मक नहीं हो सकता, अत: छोटी संख्या का वर्ग = 144
अत: छोटी संख्या = sqrt(144) = 12
संख्याएँ 12 और 18 हैं
(ग) सिद्ध कीजिए कि किसी वृत्त के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समान्तर होती हैं ।
Ans:
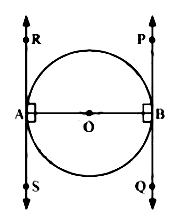
मान लिया कि O केन्द्र वाला एक वृत्त है।
मान लिया कि AB इस वृत्त का व्यास है।
मान लिया RS और PQ वृत्त के व्यास AB के दोनों सिरों पर खींची गयी स्पर्श रेखाएँ हैं।
अत: प्रमाणित करना है कि RS और PQ समांतर हैं।
चूँकि RS बिन्दु A पर वृत्त की एक स्पर्श रेखा है तथा OA उसी वृत्त की त्रिज्या है।
∴ OA ⊥ RS
∴ ∠ OAR = 90°
और, ∠ OAS = 90°
उसी तरह, OB उसी वृत्त की दूसरी त्रिज्या है तथा PQ वृत के बिन्दु B पर स्पर्श रेखा है।
अत:, OB ⊥ PQ
और ∠ OBP = OBQ = 90°
अब, ∠ OAR = ∠ OBQ = 90° [एकांतर अंत: कोणों के युग्म हैं।]
और ∠ OAS = ∠ OBP = 90° [एकांतर अंत: कोण हैं।]
चूँकि एकांतर अंत: कोण RS और PQ बराबर है।
अत: RS समांतर है PQ के
अत: किसी वृत के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समांतर होती हैं।
(घ) सिद्ध कीजिए कि किसी बाह्य बिन्दु से किसी वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिन्दुओं को मिलाने वाले रेखाखण्ड द्वारा केन्द्र पर अंतरित कोण का सम्पूरक होता है ।
Ans: दिया गया है: PA और PB एक बिंदु P से O केंद्र वाले वृत्त पर खींची गई स्पर्श रेखा हैं। साथ ही, रेखा खंड OA और OB भी खींचे गए हैं।
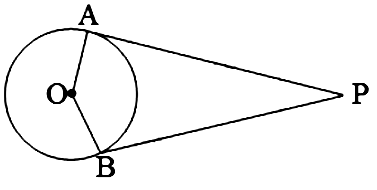
साबित करना: ∠APB + ∠AOB = 180°
उपपत्ति: हम जानते हैं कि वृत्त की स्पर्श रेखा संपर्क बिंदु से जाने वाली त्रिज्या पर लम्ब होती है।
∴ PA ⊥OA ⇒ ∠OAP = 90°, and
PB ⊥ OB ⇒ ∠OBP = 90°.
∴ ∠OAP + ∠OBP = 90°.
इसलिये, ∠APB + ∠AOB = 180°
[∵ चतुर्भुज के सभी कोणों का योग 360° होता है]
(ड़) एक थैले में 3 लाल और 5 काली गेंदे हैं। इस थैले में से एक गेंद यादृच्छया निकाली जाती है। इसकी प्रायिकता क्या है कि गेंद (i) लाल हो? (ii) लाल नहीं हो ?
Ans: यहाँ पर,
थैले में लाल गेंदों की संख्या = 3
थैले में काली गेंदों की संख्या = 5
थैले में गेंदों की कुल संख्या = 3 + 5 = 8
∴ सभी संभव परिणामों की संख्या = 8
(i) लाल गेंदों के अनुकूल परिणामों की संख्या = 3
∴ P(लाल गेंद हो) = 3/8
(ii) P(लाल गेंद नहीं हो) = 1 - 3/8
= 8 - 3/8 = 5/8
(च) नीचे दिए हुए बंटन का माध्यक 28.5 है। यदि बारम्बारताओं का योग 60 हो तो x और y के मान ज्ञात कीजिए ।
| वर्ग अन्तराल | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| बारंबारता | 5 | x | 20 | 15 | y | 5 |
Ans: दिए गए डेटा के लिए संचयी आवृत्ति की गणना निम्नानुसार की जाती है
| कक्षा अन्तराल | आवृत्ति | संचयी आवृत्ति |
| 0 - 10 | 5 | 5 |
| 10 - 20 | x | 5+ x |
| 20 - 30 | 20 | 25 + x |
| 30 - 40 | 15 | 40 + x |
| 40 - 50 | y | 40+ x + y |
| 50 - 60 | 5 | 45 + x + y |
| कुल (n) | 60 |
तालिका से यह देखा जा सकता है कि n = 60
45 + x + y = 60
x + y = 15 (1)
आँकड़ों का माध्यक 28.5 के रूप में दिया गया है जो अंतराल 20 - 30 में स्थित है।
अत: माध्यिका वर्ग = 20 - 30
माध्यिका वर्ग की निचली सीमा (L) = 20
माध्यिका वर्ग के पूर्ववर्ती वर्ग की संचयी बारंबारता (cf) = 5 + x
माध्यिका वर्ग की बारंबारता (f) = 20 वर्ग आकार (एच) = 10

3. दो अंकों की एक संख्या एवं उसके अंको को उलटने पर बनी संख्या का योग 66 है। यदि संख्या के अंकों का अन्तर 2 हो तो संख्या ज्ञात कीजिए। ऐसी संख्याएँ कितनी हैं ?
Ans: माना दहाई का अंक = x
तथा इकाई का अंक = y
मूल संख्या = 10x + y
तथा अंकों को बदलने पर प्राप्त संख्या = 10 y + x
प्रश्नानुसार,
पहली शर्त, 10x + y + 10y + x = 66
11x + 11y = 66
11(x + y) = 66
x + y = 66/11
x + y = 6 ……..(1)
दूसरी शर्त, x – y = 2 ……(2)
समी० (1) व (2) को जोड़ने पर,
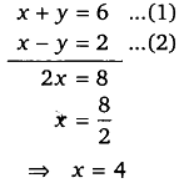
x का मान समी० (1) में रखने पर,
4 + y = 6
या y = 6 – 4 ⇒ y = 2
अतः अभीष्ट संख्या = 10x + y
= 10 × 4 + 2
= 40 + 2 = 42
अथवा
पाँच वर्ष पूर्व नूरी की आयु सोनू की आयु की तीन गुनी थी। दस वर्ष पश्चात् नूरी की आयु सोनू की आयु की दो गुनी हो जायेगी । नूरी और सोनू की आयु कितनी है ?
Ans: माना नूर की वर्तमान आयु = x वर्ष
और सोनू की वर्तमान आयु = y वर्ष
5 वर्ष पहले,
नूर की आयु = ( x - 5 ) वर्ष
सोनू की आयु = ( y - 5 ) वर्ष
प्रश्नानुसार,
x - 5 = 3( y - 5 )
⇒ x - 5 = 3y - 15
⇒ x - 3y = -10
10 वर्ष बाद,
नूर की आयु = ( x + 10 ) वर्ष
सोनू की आयु = ( y + 10 ) वर्ष
प्रश्नानुसार,
x + 10 = 2( y + 10 )
⇒ x + 10 = 2y + 20
⇒ x - 2y = 10
x - 3 y = - 10 ...(i)
x - 2y = 10 ...(ii)
समीकरण (i) से
x - 3y = - 10
⇒ x = 3y - 10 ...(iii)
x का मान समीकरण (ii) में रखने पर
x - 2y = 10
⇒ 3y - 10 - 2y = 10
⇒ y = 20
y का मान समीकरण (iii) में रखने पर
x = 3y - 10
= 3 ( 20 ) - 10
= 60 - 10 = 50
तो, नूर की आयु = 50 वर्ष
सोनू की आयु = 20 वर्ष
4. भूमि के एक बिन्दु P से एक 10 मी0 ऊँचे भवन के शिखर का उन्नयन कोण 30° है। भवन के शिखर पर एक ध्वज को लहराया गया है और P से ध्वज के शिखर का उन्नयन कोण 45° है । ध्वजदंड की लम्बाई और बिन्दु P से भवन की दूरी ज्ञात कीजिए । (√3 = 1.732)
Ans: AB भवन की ऊँचाई है, BD ध्वज दंड है । ध्वज दंड DB तथा बिन्दु P से भवन की दूरी PA ज्ञात करनी है ।

5. एक बर्तन एक उल्टे शंकु के आकार का है। इसकी ऊँचाई 8 सेमी0 है और इसके ऊपरी (जो खुला हुआ है) सिरे की त्रिज्या 5 सेमी0 है। यह ऊपर तक पानी से भरा हुआ है। जब इस बर्तन में सीसे की कुछ गोलियाँ जिनमें प्रत्येक 0.5 सेमी० त्रिज्या वाला एक गोला है, डाली जाती है तो इसमें से भरे हुये पानी का एक चौथाई भाग बाहर निकल जाता है। बर्तन में डाली गयी सीसे की गोलियों की संख्या ज्ञात कीजिए ।
Ans:
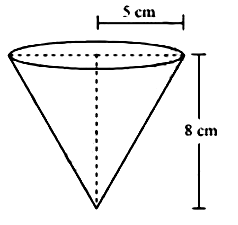
शंक्वाकार बर्तन की ऊँचाई (h) = 8 cm
शंक्वाकार बर्तन की त्रिज्या (r1) = 5 सेमी
लीड शॉट्स की त्रिज्या (r2) = 0.5 cm
बता दें कि जहाज में कई लीड शॉट गिराए गए थे।
गिराए गए पानी का आयतन = गिराए गए लेड शॉट्स का आयतन

अथवा
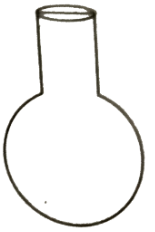
एक गोलाकार काँच के बर्तन की एक बेलन के आकार की गर्दन है जिसकी लम्बाई 8 सेमी0 है और व्यास 2 सेमी0 है जबकि गोलाकार भाग का व्यास 8.5 सेमी0 है। इसमें भरे जा सकने वाले पानी की मात्रा माप कर, एक बच्चे ने यह ज्ञात किया कि इस बर्तन का आयतन 345 वर्ग सेमी0 है। जाँच कीजिए कि उस बच्चे का उत्तर सही है या नहीं, यह मानते हुए कि उपरोक्त मापन आंतरिक मापन है । ( = 3.14)
Ans:

Read Also -
UP Board 10th Exam 2024 : सामाजिक विज्ञान अध्याय वार नोट्स & Important Question; पीडीएफ डाउनलोड करें
यहां कुछ सुझाव दिए गए हैं जो आपको यूपी बोर्ड 10वीं परीक्षा में गणित में अच्छे अंक प्राप्त करने में मदद करेंगे:
- गणित के सभी अध्यायों को अच्छी तरह से पढ़ें और समझें।
- पिछले वर्षों के प्रश्न पत्रों का अभ्यास करें।
- गणित से संबंधित समाचारों और घटनाओं के बारे में जागरूक रहें।
- अपने शिक्षकों और दोस्तों से मदद लें।
अगर आप इन सुझावों का पालन करते हैं, तो आपको यूपी बोर्ड 10वीं परीक्षा में गणित में अच्छे अंक प्राप्त करने में कोई कठिनाई नहीं होगी।
UP Board Class 10 Study Material
| UP Board Class 10 Study Material | |
| UP Board Class 10 Syllabus | UP Board Class 10 Books & Solutions |
| UP Board Class 10 Books | |







 Profile
Profile Signout
Signout












 Quiz
Quiz
 Get latest Exam Updates
Get latest Exam Updates 










