CBSE Class 10 Maths 2024-25: Chapter 4 Quadratic Equations Important Competency-Based Questions with Answers; Download Free PDF

SHARING IS CARING
If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.
As the CBSE Class 10 board exams get closer, it’s important for students to understand the new exam pattern. Starting in the 2024-25 school year, CBSE will include 50% more competency-based questions. These questions will be both multiple choice and written, focusing on how to use what students have learned in real-life situations.
This article explores Chapter 4 Quadratic Equations. It highlights key competency-based questions and provides answers to help students succeed.
Understanding Competency-Based Questions in Chapter 4: Quadratic Equations
Competency-based questions are designed to see how well students can apply their knowledge in everyday life. They can come in different forms, such as case studies, true-false questions, gap-filling tasks, and long or short answer questions.
Competency-based questions in Chapter 4: Quadratic Equations go beyond memorization, encouraging critical thinking and problem-solving. These questions help students grasp concepts deeply by applying them to real-world scenarios.
CBSE Class 10 Maths Chapter 4: Quadratic Equations Important Competency-Based Questions
Multiple Choice Questions
Q.1 Which of these quadratic equations has equal roots?
1. 3 x 2 + 9 x + 3 = 0
2. x 2 - x + 1 = 0
3. x 2 + 2 x + 1 = 0
4. 4 x 2 + 8 x - 4 = 0
Answer. 3
Q.2 The quadratic equation x 2 - 7 x + 10 = 0 can also be written as __________.
1. ( x - 5)( x - 2) = 0
2. ( x + 5)( x + 2) = 0
3. ( x - 7)( x - 10) = 0
4. ( x + 7)( x + 10) = 0
Answer. 1
Q.3 The quadratic equation x 2 + 8 x + h = 0 has equal roots.
Which of these is the value of h ?
1. 8
2. 0
3. 4
4. 16
Answer. 4
Q.4 The sum of a number z and its reciprocal is 4. Which of these correctly represents the above statement?
1. z 2 + 1 = 4
2. z 2 + z = 4
3. z 2 + 1 = 4 z
4. z 2 + 1 = -4 z
Answer. 3
Q.5 Which among the following equations can be categorized as a quadratic equation?
1. x ( x + 2) 2 = 50
2 .4 x 2 = (2 + x )(4 x - 7)
3. 3 x 2 + 5 x = 9 x ( x - 3)
4. x 2 + 1/x = 0
Answer. 3
Q.6 Look at the quadratic equation below:
- y 2 + 8 y - 18 = 0
Which of these can be said about the nature of roots of the above quadratic equation?
1. Real and unequal roots
2. Real and equal roots
3. No real roots
4. Cannot say
Answer. 3
| Download PDF | |
| CBSE Class 10 Maths Chapter 1 Real Number: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 2 Polynomials: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variable: Important Competency-Based Questions | Click Here |
| CBSE Class 10 Maths Chapter 4 Quadratic Equations: Important Competency-Based Questions | Click Here |
Q.7 Which of these equations will definitely have NO real roots, for any value of a and b other than zero?
i) 2 x 2 - bx - b 2 = 0
ii) a 2 x - ax + 2 = 0
iii) x 2 + ax + b = 0
1. only i
2. only ii
3. only iii
4. both i and ii
Answer. 2
Q.8 In the quadratic equation 6 x 2 - gx + 2 = 0, the sum of the roots is equal to three times their product. What is the value of g ?

Answer. 4
Free Response Questions
Q.9 Given below is an equation, where p is a real number.
px 2 + 4 x + 4 = 0
For what value of p will this equation not be a quadratic equation? Justify your answer.
Answer.
Mentions that for p = 0, the equation will not be a quadratic equation.
Reasons that as p = 0 will make the term with degree 2 zero, the equation will turn into a linear equation.
Q.10 Frame a quadratic equation with roots that add up to 15 and has a product of 28.
Answer. Frames a quadratic equation using x 1 2 - (α + β) x + αβ = 0 where α and β are roots of the quadratic equation
For example, x 2 - 15 x + 28 = 0.
Q. 11 Gate 3 has been placed exactly opposite to gate 1 on the boundary of the park. The distance between gate 3 and gate 2 is 1 m more than the distance between gate 3 and gate 2.
The shortest distance between gates 1 and 2 is 29 m, find the width of the park. Show your work.
Answer. Takes the distance between gates 1 and 3 as 'x' m. Writes that the distance between 1 gates 2 and 3 is ( x + 1) m.
Applies Pythagoras theorem to the triangle formed by gates 1, 2 and 3 and frames a quadratic equation as:
x 2 + ( x + 1) 2 = 292 or x 2 + x - 420 = 0
Solves the above quadratic equation and finds the value of x as 20m.
Concludes that the width of the park is 20m.
Q.12 The caretaker of the park is attempting to plant saplings in the form of a square. That is, number of rows of saplings is the same as the number of columns of saplings. On arranging the saplings, he found that 24 saplings were still left with him. When he increased the number of rows and columns by 1, he found that he was short of 25 saplings.
Find the number of saplings available with him. Show your work.
Answer. Takes the former number of rows and columns of saplings as x and finds the number of saplings available as x 2 + 24.
Takes the latter number of rows and columns of saplings as ( x + 1) and finds the 0.5 number of saplings available as ( x + 1) 2 - 25.
Equates the above two quadratic expressions and solves for x as:
x 2 + 24 = x 2 + 1 + 2 x - 25
=> x = 24
Case Study based Questions
Answer the questions based on the information given below.
A construction company PQR pvt. ltd. signed a contract to construct a hostel building having a total of 135 rooms. The manager of company called up a meeting to decide on the design of building in an efficient way. Two employees put forward their ideas.
Employee 1 said, "the number of rooms on a floor should be 2 less than thrice the number of floors in the building."
Employee 2 said, "the number of rooms on a floor should be 3 less than double the number of floors in the building."
Q.13 Represent the design suggested by employee 1 in the form of a quadratic equation. Show your work.
Answer. Assumes the number of floors in the building to be x.
Hence, writes the number of rooms on a floor as (3 x - 2).
Frames the quadratic equation as:
x (3 x - 2) = 135
=> 3 x 2 - 2 x - 135 = 0
Q.14 Represent the design suggested by employee 2 in the form of a quadratic equation. Show your work.
Answer. Assumes the number of floors in the building to be x.
Hence, writes the number of rooms on a floor as (2 x - 3).
Frames the quadratic equation as:
x (2 x - 3) = 135
=> 2x - 3 x - 135 = 0
Q.15 Which employee suggested the practical design to construct the building? How many floors should be constructed according to that employee? Show your work and give valid reason.
Answer. Solves the quadratic equation 2 x 1 2 - 3 x - 135 = 0 to get the values of x as 9 and (-7.5).
Rejects (-7.5) as number of floors cannot be negative.
Solves the quadratic equation 3 x 2 - 2 x - 135 = 0 to get the values of x as
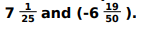
Writes that since number of floors cannot be in fraction or negative, employee 2's design is practical to construct the building.
Writes that the number of floors that should be constructed is 9.
👉 Read Also- CBSE Class 10 Half-Yearly/Mid Term 2024-25 : Most Important Questions with Answers; PDF Download (All Subjects)
👉 CBSE Class 10 Study Materials
| CBSE Class 10 Syllabus 2024-25 | NCERT Solutions For Class 10 |
| CBSE Class 10 Previous Year Question Papers | CBSE Class 10 Books |
| CBSE Class 10 Full Study Material | CBSE Class 10 Sample Paper |







 Profile
Profile Signout
Signout












 Quiz
Quiz
 Get latest Exam Updates
Get latest Exam Updates 










